Në termodinamikë, kur studiojmë kalimet nga gjendja fillestare në atë përfundimtare të një sistemi, është e rëndësishme të dihet efekti termik i procesit. Koncepti i kapacitetit të nxehtësisë është i lidhur ngushtë me këtë efekt. Në këtë artikull, ne do të shqyrtojmë pyetjen se çfarë nënkuptohet me kapacitetin izokorik të nxehtësisë së një gazi.
Gaz ideal
Një gaz ideal është një gaz, grimcat e të cilit konsiderohen si pika materiale, domethënë ato nuk kanë dimensione, por kanë masë, dhe në të cilin e gjithë energjia e brendshme përbëhet vetëm nga energjia kinetike e lëvizjes së molekulave. dhe atomet.
Çdo gaz i vërtetë në mënyrë ideale nuk do të kënaqë kurrë modelin e përshkruar, pasi grimcat e tij ende kanë disa dimensione lineare dhe ndërveprojnë me njëra-tjetrën duke përdorur lidhje të dobëta van der Waals ose lidhje kimike të një lloji tjetër. Megjithatë, në presione të ulëta dhe temperatura të larta, distancat midis molekulave janë të mëdha dhe energjia e tyre kinetike tejkalon energjinë potenciale me dhjetëra herë. E gjithë kjo bën të mundur aplikimin me një shkallë të lartë saktësie të modelit ideal për gazet reale.
Energjia e brendshme e gazit
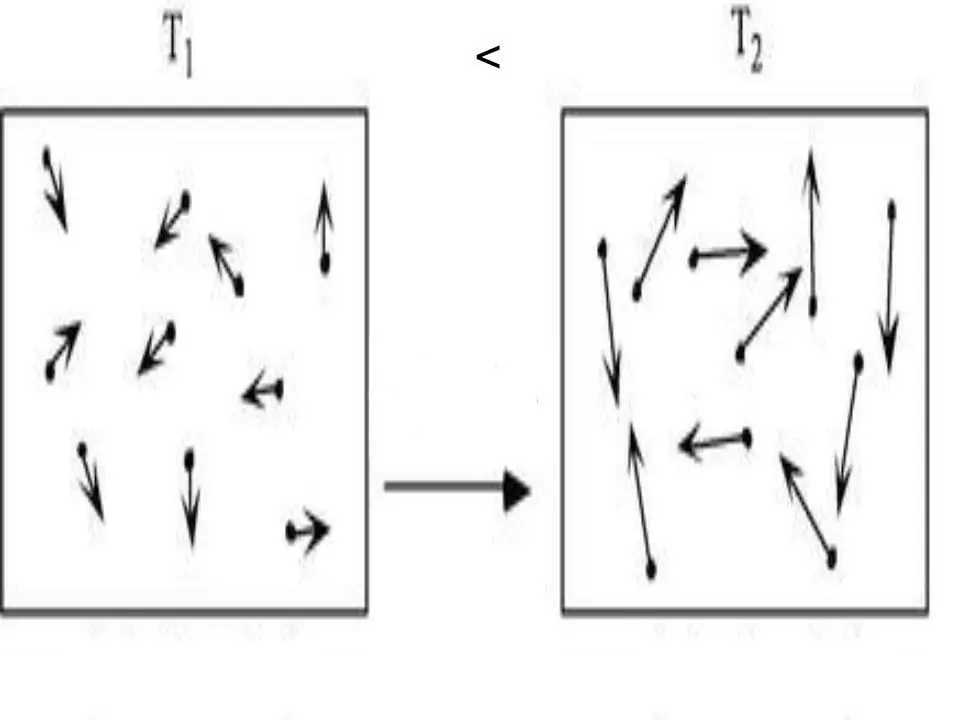
Energjia e brendshme e çdo sistemi është një karakteristikë fizike, e cila është e barabartë me shumën e energjisë potenciale dhe kinetike. Meqenëse energjia potenciale mund të neglizhohet në gazet ideale, ne mund të shkruajmë barazinë për to:
U=Ek.
Ku Ek është energjia e sistemit kinetik. Duke përdorur teorinë kinetike molekulare dhe duke zbatuar ekuacionin universal të gjendjes Clapeyron-Mendeleev, nuk është e vështirë të merret një shprehje për U. Është shkruar më poshtë:
U=z/2nRT.
Këtu T, R dhe n janë respektivisht temperatura absolute, konstantja e gazit dhe sasia e substancës. Vlera z është një numër i plotë që tregon numrin e shkallëve të lirisë që ka një molekulë gazi.
Kapaciteti i nxehtësisë izobarike dhe izokorik
Në fizikë, kapaciteti i nxehtësisë është sasia e nxehtësisë që duhet t'i sigurohet sistemit në studim për ta ngrohur atë me një kelvin. Përkufizimi i kundërt është gjithashtu i vërtetë, domethënë, kapaciteti i nxehtësisë është sasia e nxehtësisë që lëshon sistemi kur ftohet me një kelvin.
Mënyra më e lehtë për një sistem është të përcaktojë kapacitetin e nxehtësisë izokorik. Kuptohet si kapaciteti i nxehtësisë në vëllim konstant. Meqenëse sistemi nuk kryen punë në kushte të tilla, e gjithë energjia shpenzohet për rritjen e rezervave të brendshme të energjisë. Le të shënojmë kapacitetin izokorik të nxehtësisë me simbolin CV, atëherë mund të shkruajmë:
dU=CVdT.
Dmth ndryshimi në energjinë e brendshmesistemi është drejtpërdrejt proporcional me ndryshimin e temperaturës së tij. Nëse e krahasojmë këtë shprehje me barazinë e shkruar në paragrafin e mëparshëm, atëherë arrijmë në formulën për CV në një gaz ideal:
СV=z/2nR.
Kjo vlerë është e papërshtatshme për t'u përdorur në praktikë, pasi varet nga sasia e substancës në sistem. Prandaj, u prezantua koncepti i kapacitetit specifik të nxehtësisë izokorik, domethënë një vlerë që llogaritet ose për 1 mol gaz ose për 1 kg. Le ta shënojmë vlerën e parë me simbolin CV, të dytën - me simbolin CV m. Për ta, ju mund të shkruani formulat e mëposhtme:
CV=z/2R;
CVm=z/2R/M.
Këtu M është masa molare.
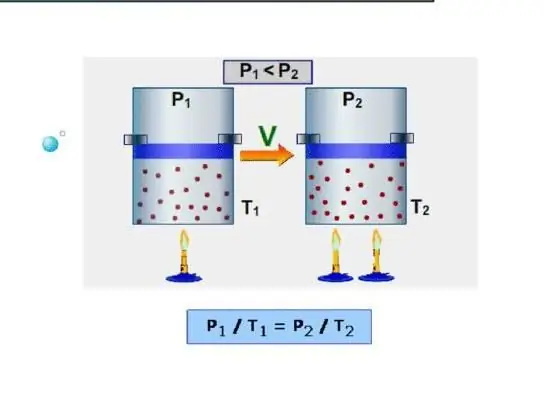
Izobarik është kapaciteti i nxehtësisë duke ruajtur një presion konstant në sistem. Një shembull i një procesi të tillë është zgjerimi i gazit në një cilindër nën një pistoni kur ai nxehet. Ndryshe nga procesi izokorik, gjatë procesit izobarik, nxehtësia e furnizuar në sistem harxhohet për të rritur energjinë e brendshme dhe për të kryer punë mekanike, pra:
H=dU + PdV.
Entalpia e një procesi izobarik është produkti i kapacitetit të nxehtësisë izobarike dhe ndryshimit të temperaturës në sistem, domethënë:
H=CPdT.
Nëse marrim në konsideratë zgjerimin në një presion konstant prej 1 mol gaz, atëherë ligji i parë i termodinamikës do të shkruhet si:
CPdT=CV dT + RdT.
Terma e fundit merret nga ekuacioniClapeyron-Mendeleev. Nga kjo barazi rrjedh lidhja ndërmjet kapaciteteve të nxehtësisë izobarike dhe izokore:
CP=CV + R.
Për një gaz ideal, kapaciteti specifik molar i nxehtësisë në presion konstant është gjithmonë më i madh se karakteristika izokore korresponduese me R=8, 314 J/(molK).
Shkallët e lirisë së molekulave dhe kapaciteti i nxehtësisë
Le të shkruajmë përsëri formulën për kapacitetin specifik molar izokorik të nxehtësisë:
CV=z/2R.
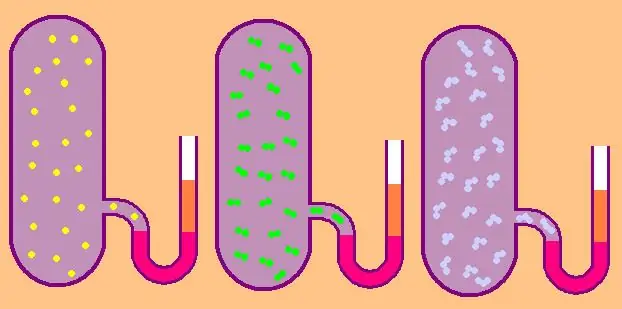
Në rastin e një gazi monoatomik, vlera z=3, pasi atomet në hapësirë mund të lëvizin vetëm në tre drejtime të pavarura.
Nëse po flasim për një gaz të përbërë nga molekula diatomike, për shembull, oksigjen O2 ose hidrogjen H2, atëherë, përveç lëvizjes përkthimore, këto molekula ende mund të rrotullohen rreth dy boshteve pingul reciprokisht, domethënë z do të jetë i barabartë me 5.
Për molekula më komplekse, përdorni z=6. për të përcaktuar CV






