Moduli i elasticitetit është një sasi fizike që karakterizon sjelljen elastike të një materiali kur një forcë e jashtme ushtrohet mbi të në një drejtim të caktuar. Sjellja elastike e një materiali nënkupton deformimin e tij në zonën elastike.
Historia e studimit të elasticitetit të materialeve

Teoria fizike e trupave elastikë dhe sjellja e tyre nën veprimin e forcave të jashtme u shqyrtua në detaje dhe u studiua nga shkencëtari anglez i shekullit të 19-të, Thomas Young. Sidoqoftë, vetë koncepti i elasticitetit u zhvillua në 1727 nga matematikani, fizikani dhe filozofi zviceran Leonhard Euler, dhe eksperimentet e para në lidhje me modulin e elasticitetit u kryen në 1782, domethënë 25 vjet para punës së Thomas Jung., nga matematikani dhe filozofi venecian Jacopo Ricatti.
Merita e Thomas Young qëndron në faktin se ai i dha teorisë së elasticitetit një pamje moderne të hollë, e cila më pas u zyrtarizua në formën e një ligji të thjeshtë dhe më pas të përgjithësuar të Hooke.
Natyra fizike e elasticitetit
Çdo trup përbëhet nga atome, ndërmjet të cilave veprojnë forcat e tërheqjes dhe të zmbrapsjes. Bilanci i këtyre forcave ështëgjendjen dhe parametrat e materies në kushte të caktuara. Atomet e një trupi të ngurtë, kur mbi to aplikohen forca të vogla të jashtme të tensionit ose ngjeshjes, fillojnë të zhvendosen, duke krijuar një forcë të kundërt në drejtim dhe të barabartë në madhësi, e cila tenton t'i kthejë atomet në gjendjen e tyre fillestare.
Në procesin e një zhvendosjeje të tillë të atomeve, energjia e të gjithë sistemit rritet. Eksperimentet tregojnë se në deformime të vogla energjia është proporcionale me katrorin e këtyre sforcimeve. Kjo do të thotë që forca, duke qenë një derivat në lidhje me energjinë, rezulton të jetë proporcionale me fuqinë e parë të sforcimit, domethënë varet në mënyrë lineare prej saj. Duke iu përgjigjur pyetjes, cili është moduli i elasticitetit, mund të themi se ky është koeficienti i proporcionalitetit midis forcës që vepron në atom dhe deformimit që shkakton kjo forcë. Dimensioni i modulit të Young është i njëjtë me dimensionin e presionit (Pascal).
Kufir elastik
Sipas përkufizimit, moduli i elasticitetit tregon se sa sforcim duhet t'i nënshtrohet një trupi të ngurtë në mënyrë që deformimi i tij të jetë 100%. Megjithatë, të gjitha trupat e ngurtë kanë një kufi elastik të barabartë me 1% sforcimi. Kjo do të thotë se nëse aplikohet një forcë e përshtatshme dhe trupi deformohet me një sasi më të vogël se 1%, atëherë pas përfundimit të kësaj force, trupi rikthen saktësisht formën dhe dimensionet e tij origjinale. Nëse aplikohet shumë forcë, në të cilën vlera e deformimit kalon 1%, pas përfundimit të forcës së jashtme, trupi nuk do të rivendosë më dimensionet e tij origjinale. Në rastin e fundit, flitet për ekzistencën e një deformimi të mbetur, që ështëdëshmi se kufiri elastik i materialit është tejkaluar.
Moduli i Young në veprim
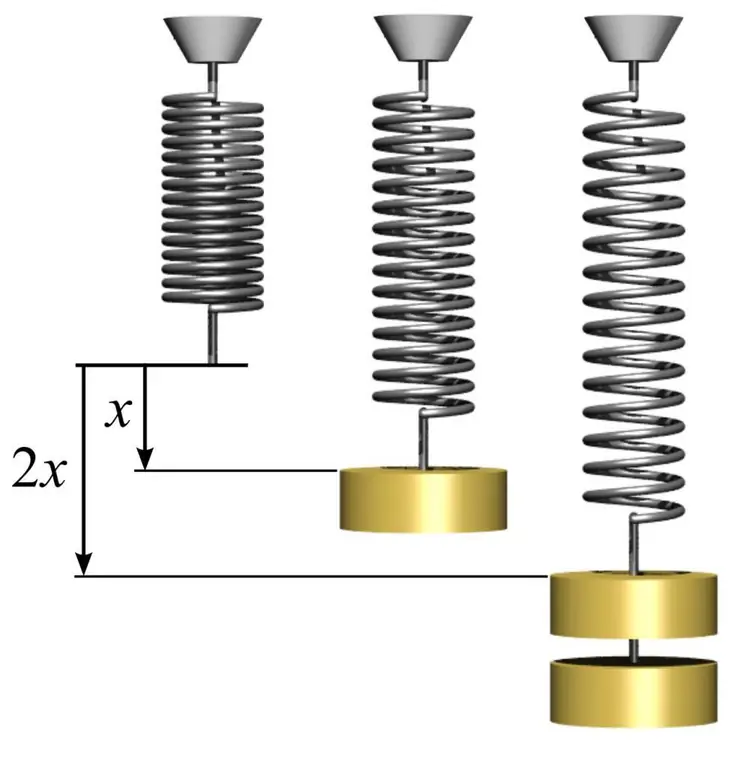
Për të përcaktuar modulin e elasticitetit, si dhe për të kuptuar mënyrën e përdorimit të tij, mund të jepni një shembull të thjeshtë me një susta. Për ta bërë këtë, ju duhet të merrni një pranverë metalike dhe të matni zonën e rrethit që formojnë mbështjelljet e saj. Kjo bëhet duke përdorur formulën e thjeshtë S=πr², ku n është pi e barabartë me 3,14 dhe r është rrezja e spirales së sustës.
Më pas, matni gjatësinë e sustës l0 pa ngarkesë. Nëse varni ndonjë ngarkesë me masë m1 në një susta, atëherë ajo do të rrisë gjatësinë e saj në një vlerë të caktuar l1. Moduli i elasticitetit E mund të llogaritet bazuar në njohuritë e ligjit të Hooke me formulën: E=m1gl0/(S(l 1-l0)), ku g është nxitimi i rënies së lirë. Në këtë rast, vërejmë se sasia e deformimit të sustës në rajonin elastik mund të kalojë shumë 1%.
Njohja e modulit të Young ju lejon të parashikoni sasinë e deformimit nën veprimin e një stresi të veçantë. Në këtë rast, nëse varim një masë tjetër m2 në susta, marrim vlerën e mëposhtme të deformimit relativ: d=m2g/ (SE), ku d - deformim relativ në rajonin elastik.
Izotropia dhe anizotropia
Moduli i elasticitetit është një karakteristikë e një materiali që përshkruan forcën e lidhjes midis atomeve dhe molekulave të tij, megjithatë një material i veçantë mund të ketë disa modula të ndryshme të Young.
Fakti është se vetitë e çdo trupi varen nga struktura e tij e brendshme. Nëse vetitë janë të njëjta në të gjitha drejtimet hapësinore, atëherë bëhet fjalë për një material izotropik. Substancat e tilla kanë një strukturë homogjene, kështu që veprimi i një force të jashtme në drejtime të ndryshme mbi to shkakton të njëjtin reagim nga materiali. Të gjitha materialet amorfe janë izotropike, të tilla si goma ose qelqi.
Anizotropia është një fenomen që karakterizohet nga varësia e vetive fizike të një ngurte ose të lëngshme nga drejtimi. Të gjitha metalet dhe lidhjet e bazuara në to kanë një ose një tjetër rrjetë kristalore, domethënë një rregullim të rregulluar dhe jo kaotik të bërthamave jonike. Për materiale të tilla, moduli i elasticitetit ndryshon në varësi të boshtit të veprimit të stresit të jashtëm. Për shembull, metalet me simetri kubike, si alumini, bakri, argjendi, metalet zjarrduruese dhe të tjera, kanë tre modula të ndryshme të Young.
Moduli i prerjes
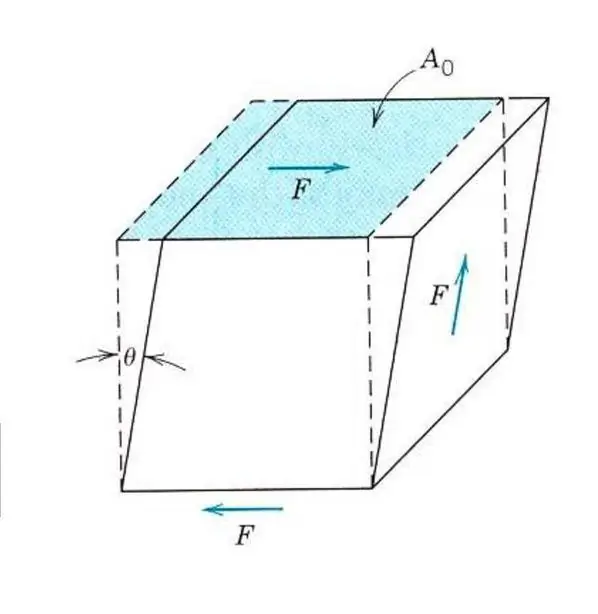
Përshkrimi i vetive elastike edhe të një materiali izotropik nuk kërkon njohuri për një modul të Young. Sepse, përveç tensionit dhe ngjeshjes, materiali mund të ndikohet nga sforcimet prerëse ose sforcimet përdredhëse. Në këtë rast, ai do të reagojë ndryshe ndaj forcës së jashtme. Për të përshkruar deformimin elastik të prerjes, është paraqitur një analog i modulit të Young-it, modulit të prerjes ose modulit të elasticitetit të llojit të dytë.
Të gjitha materialet i rezistojnë sforcimeve të prerjes më pak se tensioni ose ngjeshja, kështu që vlera e modulit të prerjes për to është 2-3 herë më e vogël se vlera e modulit të Young. Kështu, për titanin, moduli i Young-it të të cilit është i barabartë me 107 GPa, moduli i prerjes ështëvetëm 40 GPa, për çelikun këto shifra janë përkatësisht 210 GPa dhe 80 GPa.
Moduli i elasticitetit të drurit

Druri është një material anizotropik sepse fijet e drurit janë të orientuara në një drejtim specifik. Është përgjatë fibrave që matet moduli i elasticitetit të drurit, pasi është 1-2 rend madhësie më i vogël në të gjithë fibrat. Njohja e modulit të Young-it për drurin është e rëndësishme dhe merret parasysh gjatë projektimit të strukturave të paneleve prej druri.
Vlerat e modulit të elasticitetit të drurit për disa lloje pemësh janë paraqitur në tabelën më poshtë.
| Pamje peme | Moduli i Young në GPa |
| pema e dafinës | 14 |
| Eukalipt | 18 |
| Kedri | 8 |
| bredh | 11 |
| Pine | 10 |
| Lisi | 12 |
Duhet të theksohet se vlerat e dhëna mund të ndryshojnë deri në 1 GPa për një pemë të caktuar, pasi moduli i saj Young ndikohet nga dendësia e drurit dhe kushtet e rritjes.

Modulet e prerjes për lloje të ndryshme pemësh janë në intervalin 1-2 GPa, për shembull, për pishën është 1,21 GPa, dhe për lisin 1,38 GPa, domethënë druri praktikisht nuk i reziston streseve të prerjes. Ky fakt duhet të merret parasysh në prodhimin e strukturave mbajtëse prej druri, të cilat janë projektuar për të punuar vetëm në tension ose në shtypje.
Karakteristikat elastike të metaleve
Kur krahasohet me modulin e Young-it të drurit, vlerat mesatare të kësaj vlere për metalet dhe lidhjet janë një renditje e madhësisë më e madhe, siç tregohet në tabelën e mëposhtme.
| Metal | Moduli i Young në GPa |
| Bronz | 120 |
| Bakër | 110 |
| Çeliku | 210 |
| Titanium | 107 |
| Nikeli | 204 |
Vetitë elastike të metaleve që kanë singoni kubike përshkruhen nga tre konstante elastike. Metalet e tilla përfshijnë bakër, nikel, alumin, hekur. Nëse një metal ka një singoni gjashtëkëndore, atëherë nevojiten gjashtë konstante për të përshkruar karakteristikat e tij elastike.
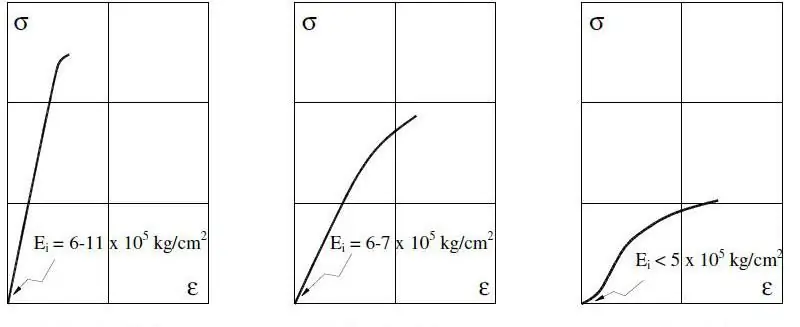
Për sistemet metalike, moduli i Young matet brenda sforcimit 0.2%, pasi vlera të mëdha mund të ndodhin tashmë në rajonin joelastik.






